Írta: Borbás Miklós
Ezen az oldalon a reakciómentes erő egy másik lehetséges előállítási módjával ismerkedhetsz meg. Miklós már nem csak elméletileg foglalkozott a reakciómentes erővel, hanem a gyakorlatban is megépített egy kísérleti, működő példányt. Erről olvashatsz a következő sorokban.
Kutatásaimban az elektromos energia közvetlen mechanikai energiává való átalakításával foglalkoztam. Kiindulásként a Thomas Brown féle 2,949,550 lajstromszámú szabadalmat használtam. Meglepő észrevételekre tettem szert: A különböző elektrosztatikus rendszerekben magasfeszültségen “reakciómentes" erő jelentkezett.
Ez azt jelenti, hogy az anód és katód nem teljesen egyforma erővel “vonzzák" egymást, az egyik erő nagyobb. A két erő különbségét nevezem reakciómentes erőnek. A kiegyensúlyozatlan erőviszony azt eredményezi, hogy az egész rendszerre egy irányba ható erő jelentkezik, mely igyekszik mozgásba hozni a rendszert.
Ezt a jelenséget 3 hasonló típusú elektromechanikus meghajtó elkészítésére használtam fel a következő módon:
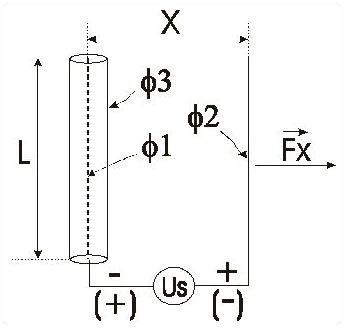
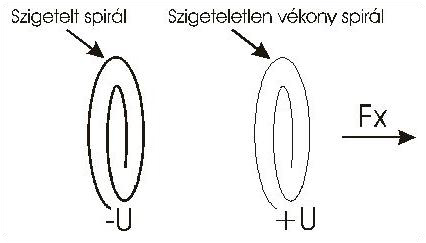
- Elhelyeztem egymástól párhuzamosan egy szigetelt drótot valamint szigeteletlen hajszáldrótot. Hajszáldrót helyett lehet olyan vezető felületet, alkalmazni amelynek éle van. Magasfeszültségre feltöltve a szigetelt dróttól a szigeteletlen felé erő jelentkezik. Ez igyekszik mozgásba hozni a rendszert, lásd az 1.ábrát és a 2. ábrát. Az ábrákon Fx-el jelöltem ezt a “reakciómentes" erőt.
- Ilyen erőt úgy is létre tudtam hoztam, hogy a szigetelt drót helyett szigetelt felületet használtam, ez is egy elektromechanikus meghajtót alkot (a rendszer a szigeteletlen vékony drót irányába igyekszik mozogni).
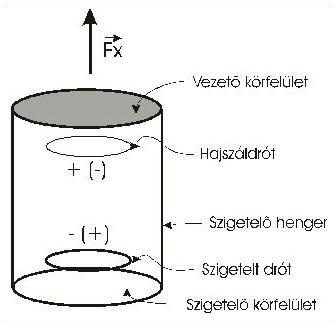
- A rendszereket hermetikusan lezárva (3. ábra) szintén elektromechanikus meghajtót hoztam létre, csak ez valamivel kisebb erővel igyekezett mozgásba lendülni.
A hermetikus leszigeteltség bizonyítja az erő reakciómentes mivoltát mivel az elektródákat körülvevő médium nem mozoghat a lezárt térben. Lezáráskor a szigeteletlen vékony drót irányából kívül-belül vezető felületet (3. ábra), míg a többi irányból szigetelő felületeket helyeztem. Így jött létre a legnagyobb mértékű reakciómentes erő.
Az alábbi ábrákon néhány példa látható reakciómentes erőt létrehozó rendszerekről:
1.ábra
2.ábra
A reakciómentes erő (Fx) jellemzői:
- Függ a polaritástól. Akkor a nagyobb az erő amikor a szigeteletlen hajszáldrót (vagy éles felület) a pozitív. Fordított polaritásnál is a szigeteletlen hajszáldrót felé jelentkezik az erő, csak akkor kisebb. Egyes körülzárt rendszereknél, melyeknél ha a szigeteletlen hajszáldrót a negatív, meg is fordulhat az erő iránya ellenkező irányba és így már a szigeteletlen hajszáldrót felől a szigetelt elektróda felé fog hatni.
- A vezetékek egymás közötti távolságának (X) növelésével egy bizonyos mértékig nő, majd pedig csökken az erő. 50 kV-on az optimális távolság 12 cm.
- A szigetelésen átáramló szivárgó áramtól csökken, sőt meg is fordulhat az iránya. Nulla áramnál a legnagyobb. Ezt kísérleteimben tapasztaltam. Ha tehát a szigetelt elektróda szigetelőanyaga nem túl jó és az elektródák elég közel vannak egymáshoz, akkor a rendszeren keresztül áram folyhat és megfordulhat az erő iránya.
- Ha a hajszáldrótok szabad végei ellenkező irányba állnak a szigetelt vezetéktől, megfordul az erő iránya.
- A szigetelt vezeték lehet szigeteletlen egy őt körülvevő szigetelő felületben (4.ábra). Ez azt jelenti, hogy ha a két szigeteletlen elektróda közül az egyiket behelyezzük egy szigetelőanyagból lévő dobozba, akkor ettől az elektródától a szabadban lévő felé fog hatni a reakciómentes erő.
- Az erő az elektródák közötti feszültség négyzetével arányos. Ezt kísérletekkel állapítottam meg.
- Az f1/f2 növekedésével nő: minél kisebb a f2, annál nagyobb az erő. Pl. 50 kV-on f1 = 1 mm, f2 = 0,15 mm, f3 = 2 mm. Ezt a jelenséget is a kísérleteim során tapasztaltam.
- A rendszert körbe lehet zárni oly módon, hogy a szigeteletlen hajszáldrót oldalán vezető felület, a többi oldal pedig szigetelő kell hogy legyen (3. ábra).
3. ábra
(a szerkezetet a fent ábrázolt módon lehet körülzárni)

4. ábra
A rendszer lényeges különbsége a Thomas Brown féle rendszerektől az, hogy szigeteletlen felület helyett szigetelt vezeték illetve szigetelt elektróda van használva és így megoldható a szerkezet érintésvédelme az 5. ábra alapján.
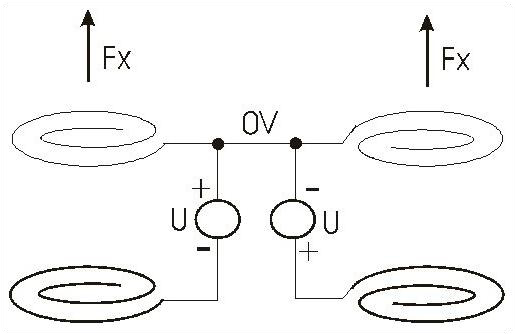
5. ábra
Szimmetrikus rendszerben a “kint lévő" szigeteletlen hajszáldrótok földhöz képesti potenciálja lehet nulla. Tehát a “lebegő" tápfeszültség forrást meg lehet úgy alkotni, hogy a szigeteletlen vezetékek földhöz képesti potenciálja nullához tartson (pl. 5. ábra).
A reakciómentes erő kérdést vet fel az energia-megmaradás törvényében, mert egy szabadban, légüres térben konstans befektetett teljesítménnyel (ami tarthat a nullához) a szerkezet folyamatosan egyenletesen gyorsulna, a sebessége az időben lineárisan nőne, így időben négyzetesen nőne a kinetikai energiája. Elérkezne az az időpont amikor a kinetikai energiája nagyobb lenne a befektetett energiától. Az energia-megmaradás törvénye csak valamilyen, a vákuumban létező energiával magyarázható, ugyanis a szerkezet kinetikai energiája arányos az “átfutott" térfogat méretével. Ez azt jelenti, hogy ha a szerkezet keresztmetszete S, bizonyos időben X távolságot tett meg vákuumban, konstans táplálással (ami a nulla áram miatt tart a nullához) akkor a kinetikai energiája arányos S * X-el.
A meghajtó rajza a legutóbbi kísérleteim szerint:

6. ábra. Egy másik lehetséges kialakítás
A térhajtómű felhasználási lehetőségei:
- Űrhajók, szatellitek meghajtása (a rakéta meghajtással ellentétben sohasem ürülne ki az üzemanyagtartály, mert ez a meghajtás nem “lövell" ki anyagot az űrhajóból vagy a szatellitből).
- Helyből felszálló repülőgép meghajtása (elég nagy feszültségen felemelhet egy repülőgépet, a feszültség pedig lehet nagy a szigetelt elektróda miatt, ellentétben a Thomas Brown féle meghajtással).
- Általánosan hangtalan mozgást létrehozó meghajtásra (pl. hangtalan tengeralattjáró).
- Villanyáram előállítása (gyorsan, vákuumban forgatva a generátort). Mivel vákuumban bizonyos idő után egy erre kialakított forgó rendszer forgási sebessége nagyobb lehet az össz befektetett energiánál, a különbséggel meg lehetne “csapolni" a rendszert).
A reakciómentes erő magyarázata:
A tér energiasűrüsége konstans. Ez az energia az elektromágneses és a nullpont energia összege. A magasfeszültségű rendszer kialakítása folytán a szigeteletlen vékony elektróda éleinél és hegyénél valamivel nagyobb lesz az elektromos tér energia sűrüsége mint a környezetben, így itt ritkább lesz a nullpont energia sűrüsége. Ennek következménye hogy reakciómentes erő keletkezik abba az irányba amerre ritkább a nullpont energia sűrüség. A rendszert tehát a nullpont energia "tolja" a hajszáldrótok hegyein keresztül. A nullpont energia sűrüsége a hajszáldrótok hegyes végeinél a legkisebb, így mikor azok ellenkező irányba állnak a szigetelt elektródától, megfordul az erő iránya. Kísérleteim alapján a következő egyenletet kaptam a reakciómentes erő számolására:
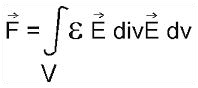
A rendszer szabadalmaztatása folyamatban van!
Befektetőt keresek szabadalmam nemzetközi levédéséhez, valamint a rendszer továbbfejlesztéséhez. Ha a szerkezet felszállna, a világűrbe is kirepülne, mert ez az effektus vákuumban is jelentkezik. Ma már elég fejlett a technika az elektronika könnyű, kis méretben való megvalósításához, hogy a szerkezet mindenestül felrepüljön.
Az eredeti anyagot itt nézheted meg.
Miklós szabadalmát elolvasva nem volt minden részlet egyértelmű, ezért ezeket levélben kérdeztem meg, s a kapott válaszok remélhetőleg számodra is egyértelművé teszik a reakciómentes erő néhány tulajdonságát.
Az első homályos dolog a reakciómentes erő felhasználása mechanikai mozgás végzésére. A forgóknál nem volt egyértelmű, hogy a szigetelt és szigeteletlen vezetékek hogy helyezkednek el. A hagyományos motoroknál van egy álló és egy forgó rész, a fent bemutatott forgóknál viszont nem volt olyan álló rész, ami lökte vagy vonzotta volna a forgórészt. Miklós a következőket írta:
"A szigetelt és szigeteletlen vezetékek együtt mozognak, de nagyobb távolságra, kb. 10 cm-re vannak egymástól, mert a reakciómentes erő bizonyos elektródák közti távolságig nő, utána csökken, mint ahogy azt feljebb már le is írtam. Érdekes, 100 kV-on még 25 cm egymás közti távolságon is majdnem maximális ez az erő. Közel egymáshoz, 1 mm távolságnál még nem jelentkezik ez az effektus.
A két elektróda pár egy rúdon egy közös tengelyre vannak erősítve, olymódon, hogy a nyomatékuk összeadódjon. Azért használtam két párt, hogy súlypontilag egyensúlyban legyen a forgó rész.
Ha nem lennének tengelyre erősítve, egyenes irányú mozgást végeznének, pl. szabadon a világűrben folyamatosan gyorsulnának. Azért erősítettem őket a forgó tengelyre, mert ez az erő még 100 kV-on is kicsi, felszállni nem tud, és így tudtam látványosan megjeleníteni. Egyébként a világon sok helyen kísérleteznek ún. lifterekkel, melyek felszállnak. Ezek a találmányom elődei, Thomas Brown szabadalma alapján készülnek. Viszont mivel szigeteletlenek, jelentős ion-szelet produkálnak és sokan ezzel magyarázzák
mozgásukat. Én arra jöttem rá, hogy az ion-szélen kívül egy másik effektus is jelentkezik, ugyanis teljesen lezárva is mozog. Ez a reakciómentes erő.
100 kV-on a forgóimnál pár 10 mN erő jelentkezik, de eddig még nem tudtam pontosabban lemérni. Mivel azonban a reakciómentes erő a feszültség négyzetével nő, biztató, hogy megoldható a repülőgép."
Megkértem Miklóst, hogy küldjön egy képet arról, hogyan nézhetne ki egy ilyen reakciómentes erővel mozgatott repülőgép. A következő rajzot küldte:

6. ábra. A reakciómentes erővel mozgatott repülőgép keresztmetszete

7. ábra. A reakciómentes erővel mozgatott repülőgép felülnézetben
A nagyfeszültség előállításához Miklós a következő kapcsolást használta:

8. ábra. A nagyfeszültséget előállító elektronika kapcsolási rajza
Az elektronikával kapcsolatban Miklós a következőket írta:
"Az általam használt trafó kimenetén kb. 5 kV jelenik meg. Ezt a transzformátort egy öreg színes tévéből vettem ki, így nem tudom megmondani a menetszámokat. A fő, hogy ne kaszkáddal egybeépített trafó legyen, hanem hozzáférhető legyen a magasfeszültségű tekercs. Szerintem bármely ilyen magasfeszültségű transzformátor felhasználható, mert én már 2 tápot készítettem két különböző trafóval, csak a meghajtó részük egyforma.
A 100 db ellenállás az átütő feszültség miatt kell, a hagyományos 0,6 W-os ellenállásokra általában 1 kV átütő feszültséget adnak meg, habár azok sokkal többet kibírnak.
A kondik tulajdonképpen 3 db (vagy javasolt 4 db) sorba kötött 2 kV-os 10 nF-os blokk kondi. A rajzon tévesen adtam meg az értéküket, mert sorba kötve csak 3,3 nF (vagy 2,5nF) kapacitást jelentenek, de nem baj, nagyobb értékekkel több kaszkád-fokozatot lehet építeni (kisebb lesz a feszültség veszteségük)."
A magyarázatot a következő sorokkal zárta Miklós:
"A repülőgépet 3 számítógéppel vezérelt magasfeszültséget előállító elektronika táplálja, így a 3 különböző irányba ható erő segítségével könnyen manőverezhet. A felbecsült szükséges feszültségek pár 10 MV, de mivel a minőséges szigetelőkön keresztül nem folyik áram, hatékony elektronikák segítségével a fogyasztás kicsi lehet.
A repülőgép meghajtásánál éppen az a lényeg, hogy az erő nem két tárgy között jelentkezik, hanem az egész rendszerre hat, az egész mindenestől mozog. Ez az effektus jelentkezik a forgóimnál is, ez az a
fantasztikus jelenség, a reakciómentes erő (akció reakció nélkül). Valójában a szerkezeteket a nullpont energia mozgatja. Nehéz megértenünk, mert minket másképp tanítottak az iskolákban, valamint ez a jelenség nem jelentkezik mindennapi életünkben. Ezért szeretném hirdetni ezt az újdonságot, mert szerintem ennek kivizsgálásakor még sok új jelenséget meg fogunk ismerni, ez új kapukat nyit a tudomány előtt."
Végezetül következzék egy videó, ahol Miklós bemutatja a bipoláris forgóját.
(newbipolar.wmv)Sajnos a videó hiányzik, ha valakinek megvan kérem küldje el nekem, az elérhetőségek menüpontban megadott címre!
1.videó. A működés ismertetése (8,72 MB, 5:20 perc)
Nagyon érdekesnek tűnik ez a jelenség. Ha neked is van kedved kísérletezni vele, akkor bátran állj hozzá és mondd el nekünk az eredményeidet.
Kapcsolódó kísérletek:
 TÉRSZOBRÁSZAT Energiakonverterek Blogja
TÉRSZOBRÁSZAT Energiakonverterek Blogja